Research Assistant | M.Sc. Mathematics
MAR 6.037
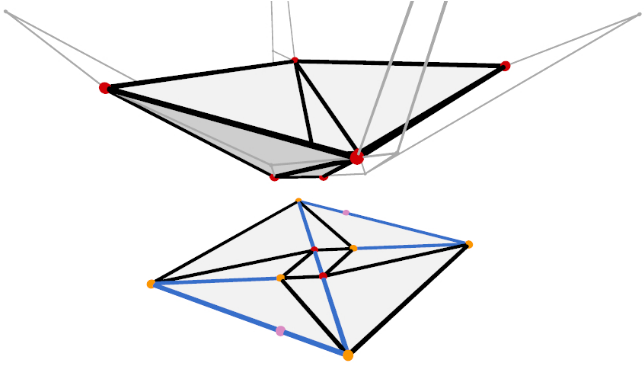 Sums of Wedges: Conforming Weighted Delaunay Triangulations are Polynomial in Fixed Dimension (2025)
ACM Transactions on Graphics (Proc. of SIGGRAPH Asia)
Sums of Wedges: Conforming Weighted Delaunay Triangulations are Polynomial in Fixed Dimension (2025)
ACM Transactions on Graphics (Proc. of SIGGRAPH Asia)
@article{10.1145/3763368,
author = {Bogiokas, Dimitrios and Finnendahl, Ugo and Seidelmann, Thorsten and Alexa, Marc},
title = {Sums of Wedges: Conforming Weighted Delaunay Triangulations are Polynomial in Fixed Dimension},
year = {2025},
issue_date = {December 2025},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {44},
number = {6},
issn = {0730-0301},
url = {https://doi.org/10.1145/3763368},
doi = {10.1145/3763368},
abstract = {We show how the problem of creating a triangulation in d-dimensional space that conforms to constraints given as sub-simplices can be turned into the problem of computing the lower hull of a sum of wedge functions. This sum can be interpreted as a Weighted Delaunay Triangulations, necessarily containing the constraints as unions of its elements. Intersections of wedges lead to Steiner points. As the number of such intersections is polynomial in the number of wedges, and the number of wedges per element is typically 1 (at most d), this proves that the complexity of the output is polynomial. Moreover, we show that the majority of wedge intersections is unnecessary for a conforming triangulation and further heuristically reduce the number of Steiner points. Using appropriate data structures, the function can be evaluated in quasi-linear time, leading to an output-sensitive algorithm.},
journal = {ACM Trans. Graph.},
month = dec,
articleno = {248},
numpages = {16}
}
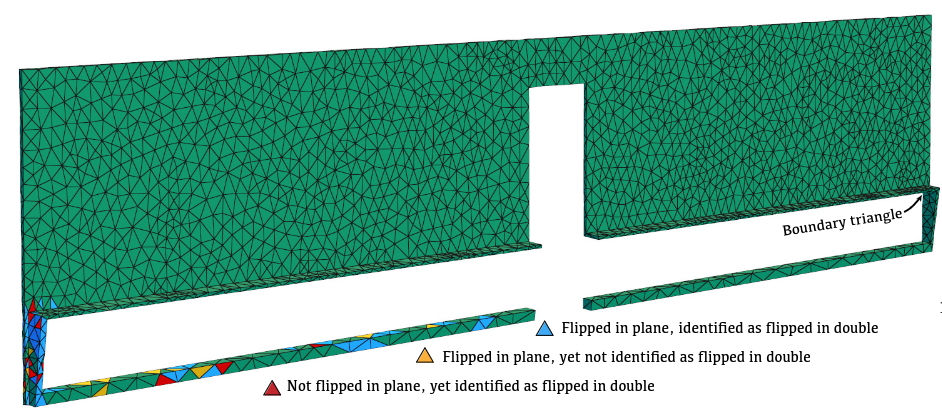 Efficient Embeddings in Exact Arithmetic (2023)
ACM Transactions on Graphics (Proc. of SIGGRAPH)
Efficient Embeddings in Exact Arithmetic (2023)
ACM Transactions on Graphics (Proc. of SIGGRAPH)
@article{10.1145/3592445,
author = {Finnendahl, Ugo and Bogiokas, Dimitrios and Robles Cervantes, Pablo and Alexa, Marc},
title = {Efficient Embeddings in Exact Arithmetic},
year = {2023},
issue_date = {August 2023},
publisher = {Association for Computing Machinery},
address = {New York, NY, USA},
volume = {42},
number = {4},
issn = {0730-0301},
url = {https://doi.org/10.1145/3592445},
doi = {10.1145/3592445},
abstract = {We provide a set of tools for generating planar embeddings of triangulated topological spheres. The algorithms make use of Schnyder labelings and realizers. A new representation of the realizer based on dual trees leads to a simple linear time algorithm mapping from weights per triangle to barycentric coordinates and, more importantly, also in the reverse direction. The algorithms can be implemented so that all coefficients involved are 1 or -1. This enables integer computation, making all computations exact. Being a Schnyder realizer, mapping from positive triangle weights guarantees that the barycentric coordinates form an embedding. The reverse direction enables an algorithm for fixing flipped triangles in planar realizations, by mapping from coordinates to weights and adjusting the weights (without forcing them to be positive). In a range of experiments, we demonstrate that all algorithms are orders of magnitude faster than existing robust approaches.},
journal = {ACM Trans. Graph.},
month = {jul},
articleno = {71},
numpages = {17},
keywords = {integer coordinates, parametrization, schnyder labeling}
}